
The most updated model of an unentangled electron and an unentangled positron with a charge field due to oscillation of its gravitational energy gradient as its 2-D electric energy moves outward from system center can be seen at this link: Charge field produced by oscillating gravitational energy gradient of an unentangled electron and of an unentangled positron.
The inherent energy of space consists of basic units of 1-D bidirectional energy in random motion and distribution relative to each other to maintain a dynamic equilibrium or directional balance of the energy system. The basic units of 1-D energy represent the potential energy of space, while the rate of motion of the 1-D units of energy constitutes the kinetic energy of space. The inherent energy of space can form magnetic energy, time energy, and gravitational gradients to provide directional balance to electric (i.e., unidirectional or nonrandom) energy.
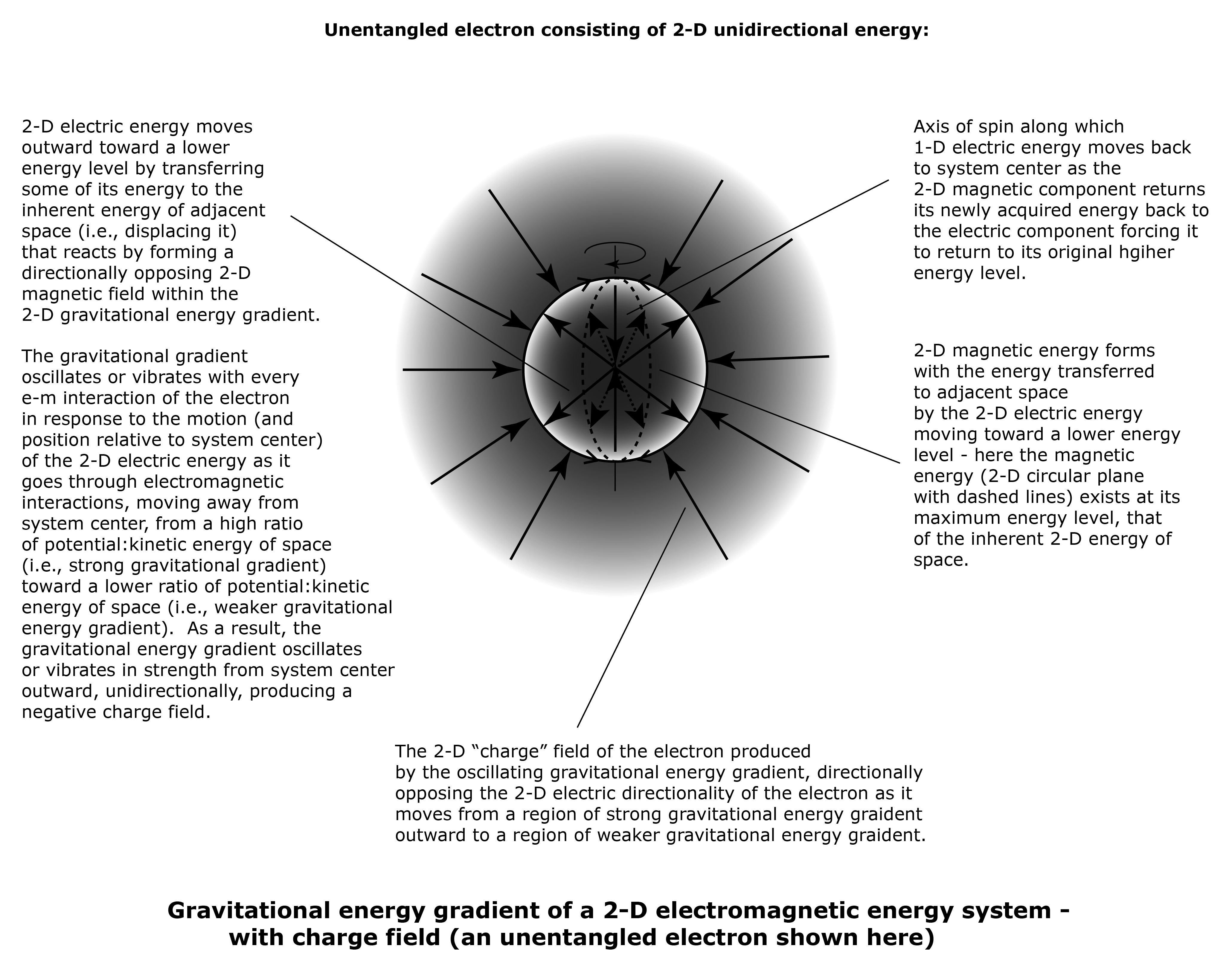
A 2-D electromagnetic (e-m) particle, such as an electron, consists of e-m interactions. Each e-m interaction goes through phases where the 2-D electric energy goes from a high energy level outward to a lower energy level and then back to its original high energy level. The overall electromagnetic phases of a 2-D electron appear to be wavelike (see Electron structure). The motion of the 2-D electric energy relative to system center causes a directional imbalance. The energy of surrounding space reacts to form 2-D magnetic energy, 2-D time energy, and a gravitational energy gradient to help provide directional balance.
In the case of a 2-D electromagnetic (e-m) particle, such as an electron or a positron, the inherent energy of space forms a 2-D gravitational energy gradient about the particle. The gravitational gradient provides directional balance to the particle with directionally opposing energy composed of a changing ratio of potential to kinetic energy of space inward toward the center of gravity. The amount of potential energy of space increases inward toward the body of mass, while the amount of kinetic energy of space decreases proportionally to maintain the directional balance of the inherent energy of space.
The gravitational gradient possesses an equal amount of total energy to that of the particle (or body of mass) for which it is providing directional balance. This means that the gravitational gradient does have a finite outer boundary (i.e., limit), and in the case of large bodies of mass, the diameter of that boundary is very large. The boundary of the gravitational energy gradient is proportional to the amount of mass and the energy density of the body of mass-energy for which it is providing directional balance.
A gravitational energy gradient provides directional balance to the density of an electron or positron relative to the density of the inherent energy of space. The 2-D electron is composed of electromagnetic energy that moves outward from system center, and recycles through a 1-D axis of spin inward to system center. Its gravitational gradient possesses a changing ratio of greater and greater potential to kinetic energy of space inward toward the center of gravity. Since the 2-D e-m energy of the electron is in motion relative to system center, it moves through its gravitational energy gradient from a high ratio of potential to kinetic energy of space at system center to a low ratio of potential to kinetic energy of space at its outer boundary (where the 2-D magnetic energy is at its highest possible energy level). As it does, the strength of the gravitational gradient essentially changes or oscillates with the motion of the e-m interaction outward from center. This results in a directional force surrounding the electron caused by the changing strength of the gravitational energy gradient with each e-m interaction of the electron. This produces the negative charge field.
The 2-D positron is composed of electromagnetic energy that moves inward to system center, and recycles through a 1-D axis of spin outward to the poles at the outer boundary of the particle (where the magnetic energy is at its highest possible energy level). Its gravitational gradient possesses a changing ratio of greater potential:kinetic energy of space inward toward the center of gravity. The strength of the gravitational gradient of a positron oscillates or vibrates with every e-m interaction, resulting in a directional force opposite that of an electron. As the 2-D electric energy of the positron moves inward toward system center it is moving through its gravitational energy gradient from a low ratio of potential: kinetic energy of space at the system boundary to a high ratio of potential:kinetic energy of space at system center. The resulting directional force caused by the oscillating gravitational energy gradient composes the positive charge field of the positron.
Using this model, the relationship between a gravitational energy gradient and an elementary electromagnetic energy system can be understood in terms of the inherent energy of space. The gravitational energy gradient consists of a changing ratio of potential to kinetic energy of space inward toward a body of mass (i.e., 2-D or 3-D e-m energy), and an elementary 2-D electromagnetic energy system consists of two 2-D planes of energy – a 2-D plane of electric energy perpendicular to a 2-D plane of magnetic energy. The strength of the gravitational energy gradient oscillates or vibrate with the e-m interactions of its elementary particle as the 2-D electric energy moves through it either away from system center or toward system center, resulting in a directional force field, or a charge field.
NOTE: See additional illustrations at the following link: Charge fields resulting from the oscillation of gravitational energy gradients of an unentangled electron and an unentangled positron.